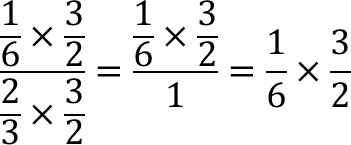分数の割り算
と言えば、やり方は、
1.÷を×になおす
2.÷の後ろを逆数にする
という2つの作業をしたうえで、
分数同士の掛け算として計算しますよね。
小学校で分数を教えるときにはこれで十分だし、
これをひたすら覚えさせるべきだと思います。
ただ、
- 逆数にする理由
- ÷が×に変わる理由
にはきちんとした論理があります。
小学生のうちにこ
のひっくり返す理由まで教えるのは
けっこう大変ではあるものの、
覚えおいて損はないんですよね。
中学生になると、今度は
マイナス同士の掛け算がどうしてプラスになるの?
という非常に説明しにくい計算も出てくるので、難しいことは考えず、
何も考えずに覚えてしまうのが手っ取り早いですよね。
関連ページ:マイナスかけるマイナス|マイナスXマイナス(掛け算)例え
むしろ分数の方程式を解くようになってから改めて、
分数の割り算のやり方を論理的に見直すことで、
基本の重要性をより深く理解させることが
できるんじゃないかと感じています。
【教えて!ガリ勉先生!】1時間目
「分数の割り算で計算する時、なんで後ろだけひっくり返さなきゃいけないの?理屈もわからないのに出来ません!!」先生「実際数字にしてみると分かりやすいニャ!掛け算しかしないから何個も割り算するよりお得な考え方が 逆数 ニャ!」 pic.twitter.com/1xNWEDxaxX
— 害 (@toxicantGai) 2017年11月4日
目次
分数の割り算でひっくり返す理由
分数の割り算を規則性から教える方法
たとえば
12 ÷ 12 = 1
12 ÷ 6 = 2
12 ÷ 3 = 4
12 ÷ 2 = 6
12 ÷ 1 = 12
という問題は、簡単に解けると思います。
12 ÷ 24 = 12/24 = 1/2
という分数の問題も、割と簡単に導き出せると思います。
ここで
「12÷12は1だったけど、12÷24で割る数が2倍になると答えが半分の1/2になったよね」
と確認をします。
その上で、
「12÷6は2で、12÷3は4。割る数が6から3に1/2になると答えが今度は2倍になってるよね。」
「では12÷1は12だったけど、12÷1/2で割る数が1/2になるとどうなると思う?」
といった感じで話をすると、答えが自然と24になることを導き出すことができ、
子供たちに逆数の概念を持ってもらえるきっかけができます。
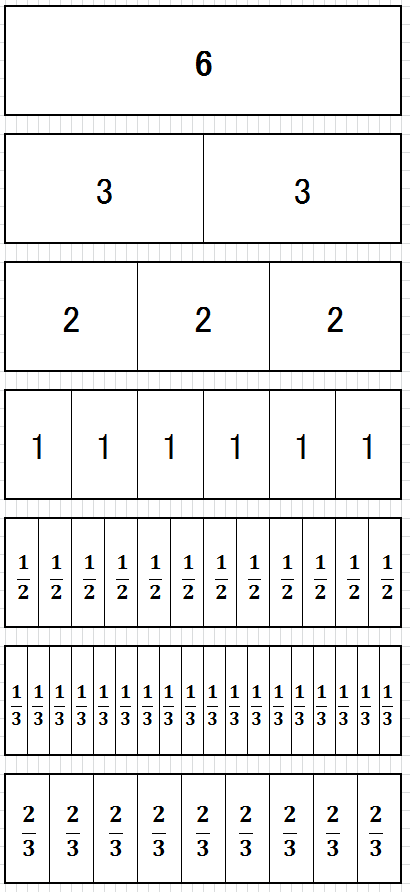
分数の割り算を箱の中に箱を入れるイメージで教える方法
6の大きさの箱の中に3の大きさの箱はいくつ入るかな?
6の大きさの箱の中に2の大きさの箱はいくつ入るかな?
6の大きさの箱の中に1の大きさの箱はいくつ入るかな?
みたいな文章問題は簡単に割り算で解けると思います。
6 ÷ 3 = 2
6 ÷ 2 = 3
6 ÷ 1 = 6
といった感じで数式にあらわすことができますが、
ココから話を発展させて、
6の大きさの箱の中に1/2の大きさの箱はいくつ入るかな?
6の大きさの箱の中に1/3の大きさの箱はいくつ入るかな?
6の大きさの箱の中に2/3の大きさの箱はいくつ入るかな?
といった問題につなげていきます。
子供にはイメージ図を通して答えを先に知ってもらい、
その上で分数の割り算を数式で表現するにはどうすれば良いのか?を考えてもらいます。
ただ考えてもらっても子供が自発的に逆数を見つけるのは難しいものがあるので、
分子と分母をひっくり返すと、結果的に正しい答えが導き出せることを覚えてもらいます。
はじき(速度計算)を使って分数の割り算を教える方法
速度計算では、
速度(時速) = 距離(Km) ÷ 時間(1時間単位)
で計算することができます。
3時間で60キロ走った時の速度は? → 60 ÷ 3 = 20
2時間で60キロ走った時の速度は? → 60 ÷ 2 = 30
1時間で60キロ走った時の速度は? → 60 ÷ 1 = 60
というのは単純な掛け算で考えることができますね。
ココから応用させて、
「30分で60キロ走った時の時速」について考えてもらいます。
1時間だと合計で120キロ走ることになるので、時速は120kmという答えが導き出せそうです。
同じように、
20分で60キロ走った時の時速
10分で60キロ走った時の時速
についても考えていくことで、
分数の割り算は逆数の掛け算で考えるきっかけをつかむことができます。
数式の変形から分数の割り算を教える方法
分数の分数を使って分数の割り算を教える方法
6分の1を3分の2で割る分数の割り算について考えていきます。
分数の割り算のやり方をそのまま当てはめるならば、
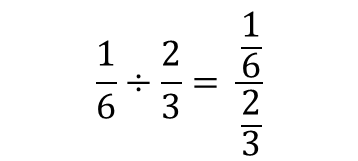
といった感じで、読みにくさはあるものの、分数の分母分子それぞれに、
分数をそのまま入れることもできます。
同じく分数の定義から考えると、
分母と分子に同じ数をかけても、
分数の値が変わることはありません。
そこで、分母に書いている分数とはちょうど逆の数字を
分母・分子療法に掛け算します。
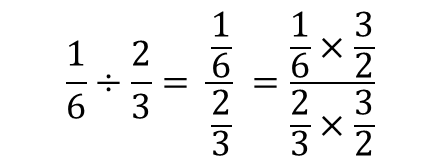
素直に計算をしていくならば、
分母にある分数の掛け算はちょうど分子・分母が相殺されて1になり、
結果的に最初の数式で「割る数」だった3分の2がひっくり返って、
2分の3になっていることを導き出すことができます。
分数の分数を使わずに数式を展開させて分数の割り算を教える方法
たとえば、
3/4 ÷ 2/5
という割り算の計算をしようと思ったら、
3/4 ÷ 2/5 = 3/4 × 5/2 = 15/8
という風に、÷の後ろの分数を逆数にして
(分子と分母をひっくり返して)掛け算で計算しますよね。
結果だけ見てみると、大した話じゃないんですが、
分数をひっくり返して逆数にする理由を明確にするために、
ひっくり返す過程をもう少しかみ砕いて見ていきます。
まずは、1をかけても計算結果はわからない、
というところからスタートしましょう。
つまり
3/4 ÷ 2/5 = 3/4 ÷ 2/5 × 1
ですよね。
ここで、1を分数同士の掛け算に分解します。
具体的には、
1 = 2/5 × 5/2
という風に考えます。
分数同士の掛け算
に分解した状態で、
元の式にあてはめると、
3/4 ÷ 2/5 × 1
=3/4 × 1 ÷ 2/5 ※1の場所をひとつ前に移動
=3/4 × (5/2 × 2/5)÷ 2/5 ※1を逆数の掛け算に分解
となります。
掛け算「X1」に関しては、
場所を移動させても問題ありませんから、
ひとつ前に移動させて分解させました。
さらに計算を進めていくと、
3/4 × (5/2 × 2/5)÷ 2/5
= 3/4 × 5/2 × 2/5 ÷ 2/5 ※()を外しただけ
= 3/4 × 5/2 ×(2/5 ÷ 2/5) ※2/5と2/5で割り算
= 3/4 × 5/2 × 1 ※同じ数同士の割り算だから1になる
= 3/4 × 5/2 ※1を省略
となりますよね。
分数の割り算では
÷を×に直して逆数の掛け算にするわけですが、
その背景にはこういったプロセスがあるわけです。
ただこの過程を小学生に説明するには、
ちょっと難易度が高いから省略。
「÷を×に直して逆数の掛け算にする」
ことだけを覚えさせてしまったほうが
スムーズだというわけですね。
日本の教育は
暗記に重点が置かれていて頭でっかちになりがち、
なんて言われますが、それは極論じゃないか?
というのが僕の独自の見解です。
通分する方法もある
逆数を避けるならば、
通分して計算する方法もあります。
例えば、整数の割り算は、
8 ÷ 4
=8/1 ÷ 4/1
=8/4
=2
といった感じで計算していると言えなくもない。笑
分母そろえることで結果として分母を相殺できるので、
分数同士の掛け算では通分するのもありっちゃあり。
3/4 ÷ 2/5
=15/20 ÷ 8/20
=15/8
分数ものさしなるものも登場!
小学生が発明し、メーカーによる商品化もされたのが、
分数ものさし。
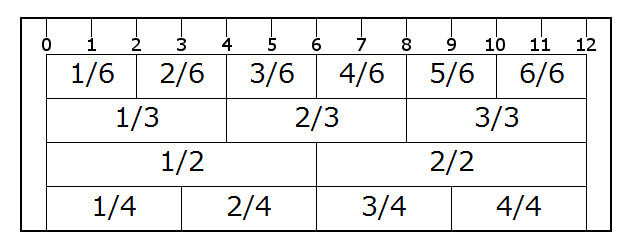
出典:https://guide-jp.com/hamamatsu/wp-content/uploads/2017/04/bunsu_m.jpg
この分数ものさしはどんなふうにつかうのかというと、
たとえば
1/6 ÷ 1/2
の場合だと、
「1/6」の一番上のメモリを見ると「2」
「1/2」の一番上のメモリを見ると「6」
になっていることがわかります。
「1/6」と「1/2」をそれぞれの数値に変換し、
2 ÷ 6 = 1/3
といった感じで整数同士の割り算で
分数計算ができるようになります。
分数ものさしを考案したのは、小学生だと言いますから、
そう考えると、これこれですごい発明だと思います。
この発想には多くの大人が驚かされたわけですが、
ただこれで分数の割り算が完全に克服できるのか?
というと、ちょっと疑問が残るんですよね。
「1/6はなぜ2なの?」
「1/4はなぜ3なの?」
と、不思議に思う子が出てきてもおかしくない訳で、
そうなると当然、説明に困っちゃいます。
説明できることはできるけれど、
通分するとか「1」を加えて計算する場合よりも、
更に説明が面倒で厄介になります。汗
途中のプロセスを理解できないと辛い
僕は塾の講師をやっていたことがあり、
小学生にも勉強を教えていました。
小学生に基本を教えることがどれだけ難しいか
身を持って理解しているつもり。
分数の割り算も、
途中計算を持ち出すのは
愚の骨頂だとわかっています。
だからこそ暗記しちゃったほうが、
教える方も教わるほうも
両方ともハッピーだとは思います。
ただいつかは、
その意味をきちんと教えてあげるべきだと
思うんですね。
親が子供に注意することっていうのも、
些細なことが多かったりするじゃないですか?
箸の持ち方や使い方、
日常生活のちょっとしたマナーなど。
子供にしてみたら、
「何でそんなことでいちいち怒るんだよ!」
って思うわけですが、
怒るにはわけがあるんですよね。
子供にマナーなんて言っても
最初は理解できないことも多いものです。
それならまずは覚えさせちゃうほうが良い、
って言う発想は、間違っちゃないし、
生産的だと思います。
ただ、なぜそうするか?
って言うのを教えてあげないと、
本当の意味で理解はできないと思うんですね。
分数の掛け算にしても、
結果だけを「計算のルール」として覚えるのは、
間違いではないとは思いますが、
なぜそうなるのか?
というのをいつかは教えてあげたほうが、
論理的に考える思考法みたいなものを、
子供に伝えることができるじゃないか?と思います。